Representing and Measuring Motion
Average Speed
In any journey the speed of the vehicle will keep changing, but its average speed can be calculated if the total distance and time taken are known.
| average speed (m/s) | = | distance travelled (m) |
|
So if a cyclist travels 600 metres in 1 minute (60 seconds) his average speed will be:
| Average speed | = | 600 |
|
|
| = | 10 m/s |
|
Distance-time Graph
If an object moves in a straight line, its distance from a certain point can be represented as a distance-time graph.

The line A-B shows a car travelling at a steady speed. It covers 2 km every 5 minutes.
Line C-D also shows a steady speed, but it is travelling slower and covers only 1 km every 5 minutes.
The gradient of the slope gives the speed of the object.
Gradient
| = | distance covered |
|
Gradient of line A-B | = | 6 km |
|
| = | 0.4 km/min |
|
Gradient of line C-D | = | 2 km |
|
| = | 0.2 km/min |
|
The steeper the slope of the graph, the greater the speed it represents.
The horizontal line, B-C, shows that the car has stopped.
The distance stays at 6 km from where the car set off.
Velocity–time Graph
Velocity is speed in a given direction.
Velocity-time graphs can represent the movement of an object.
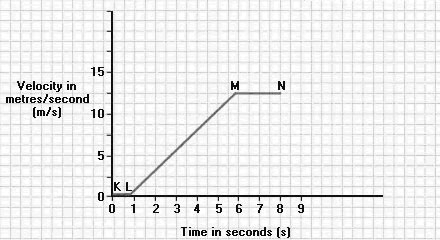
Between K and L the velocity of the car is 0 m/s. It is stopped.
Between L and M the car's velocity is increasing at a constant rate. Every second its velocity increases by 2.5 m/s.
A diagonal line shows an object is moving with constant acceleration.
The gradient of the line gives the acceleration.
Gradient of L-M | = | change in velocity |
|
| = | 12.5 |
|
|
| 5 |
|
| = | 2.5 m/s2 |
|
The steeper the slope of the line, the greater the acceleration.
Between M and N the velocity stays at 12.5 m/s.
A horizontal line shows a constant velocity.
The area under a velocity-time graph represents the distance travelled.
Area under line L-M | = | ½ x height of triangle x base of triangle |
| = | ½ x 12.5 x 5 |
| = | 31.25 |
So the car covered 31.25 m whilst accelerating.
The area under line M-N | = | height of rectangle x width of rectangle |
| = | 12.5 x 2.2 |
| = | 27.5 |
So the car travelled 27.5 m at a constant velocity. | ||
The total distance travelled | = | 31.25 + 27.5 |
| = | 58.75 m |
Acceleration and Deceleration
Acceleration is the rate at which the velocity of an object changes.
This equation is used to calculate the steady acceleration of an object, travelling in a straight line.
acceleration (m/s2) | = | change in velocity (m/s) |
|
| time taken for change (s) |
If a car accelerates from a velocity of 10 m/s to 50 m/s in 5 seconds its acceleration will be:
Acceleration | = | (50 -10) |
|
|
| 5 |
|
| = | 40 |
|
|
| 5 |
|
| = | 8 m/s2 |
|
The rate that an object's velocity decreases is called its deceleration.
It is calculated using the same equation.
If a car is travelling at 20 m/s and it comes to a halt in 5s, its deceleration is:
Deceleration | = | (20 – 0) |
|
| = | 20 |
|
| = | 4 m/s2 |
|

Between K and L the velocity of the car is 0 m/s. It is stopped.
Between L and M the car's velocity is increasing at a constant rate. Every second its velocity increases by 2.5 m/s.
A diagonal line shows an object is moving with constant acceleration.
The gradient of the line gives the acceleration.
Gradient of L-M | = | change in velocity |
|
| = | 12.5 |
|
|
| 5 |
|
| = | 2.5 m/s2 |
|
The steeper the slope of the line, the greater the acceleration.
Between M and N the velocity stays at 12.5 m/s.
A horizontal line shows a constant velocity.
The area under a velocity-time graph represents the distance travelled.
Area under line L-M | = | ½ x height of triangle x base of triangle |
| = | ½ x 12.5 x 5 |
| = | 31.25 |
So the car covered 31.25 m whilst accelerating.
The area under line M-N | = | height of rectangle x width of rectangle |
| = | 12.5 x 2.2 |
| = | 27.5 |
So the car travelled 27.5 m at a constant velocity. | ||
|
|
|
The total distance travelled | = | 31.25 + 27.5 |
| = | 58.75 m |
Acceleration and Deceleration
Acceleration is the rate at which the velocity of an object changes.
This equation is used to calculate the steady acceleration of an object, travelling in a straight line.
acceleration (m/s2) | = | change in velocity (m/s) |
|
| time taken for change (s) |
If a car accelerates from a velocity of 10 m/s to 50 m/s in 5 seconds its acceleration will be:
Acceleration | = | (50 -10) |
|
|
| 5 |
|
| = | 40 |
|
|
| 5 |
|
| = | 8 m/s2 |
|
The rate that an object's velocity decreases is called its deceleration.
It is calculated using the same equation.
If a car is travelling at 20 m/s and it comes to a halt in 5s, its deceleration is:
Deceleration | = | (20 – 0) |
|
| = | 20 |
|
| = | 4 m/s2 |
|
Document Actions

 Like us on Facebook
Like us on Facebook