Long Division with Remainders
When we are given a long division to do it will not always work out to a whole number. Sometimes there will be numbers left over. These are known as remainders.
Let’s see how it is done with 435 ÷ 25
There are two definitions we must make first.
- the number to be divided into is known as the dividend (435 from above)
- The number which divides the other number is known as the divisor (25 from above)
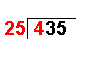 | 4 ÷ 25 = 0 remainder 4 | The first number of the dividend is divided by the divisor. |
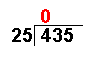 | The first number of the dividend is divided by the divisor. | |
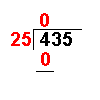 | 25 × 0 = 0 | The answer from the first operation is multiplied by the divisor. The result is placed under the number divided into. |
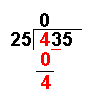 | 4 – 0 = 4 | Now we take away the bottom number from the top number. |
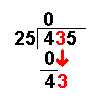 | Bring down the next number of the dividend. | |
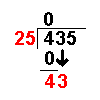 | 43 ÷ 25 = 1 remainder 18 | Divide this number by the divisor. |
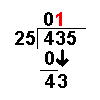 | The whole number result is placed at the top. Any remainders are ignored at this point. | |
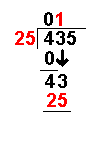 | 25 × 1 = 25 | The answer from the above operation is multiplied by the divisor. The result is placed under the last number divided into. |
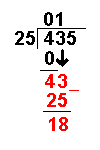 | 43 – 25 = 18 | Now we take away the bottom number from the top number. |
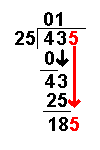 | Bring down the next number of the dividend. | |
 | 185 ÷ 25 = 7 remainder 8 | Divide this number by the divisor. |
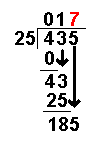 | The whole number result is placed at the top. Any remainders are ignored at this point. | |
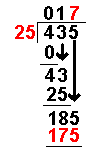 | 25 × 7 = 175 | The answer from the above operation is multiplied by the divisor. The result is placed under the number divided into. |
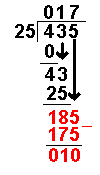 | 185 – 175 = 10 | Now we take away the bottom number from the top number. |
| There are still 10 left over but no more numbers to bring down. | ||
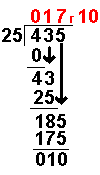 | With a long division with remainders the answer is expressed as 17 remainder 10 as shown in the diagram. |
Document Actions

 Like us on Facebook
Like us on Facebook