Introduction to Algebra - Multiplication
Another Puzzle
What is the missing number?
× | 4 | = | 8 |
The answer is 2, right? Because 2 × 4 = 8.
Well, in Algebra we don't use blank boxes, we use a letter. So we might write:
x | × | 4 | = | 8 |
But the "x" looks like the "×"! ... that could be very confusing ... so in Algebra we don't use the multiply symbol (×) between numbers and letters, we simply put the number next to the letter to mean multiply:
4x | = | 8 |
You would say in English "four x equals eight", meaning that 4 x's make 8. And the answer would be written:
x | = | 2 |
How to Solve
- Work out what to remove to get "x = ..."
- Remove it by doing the opposite
- Do that to both sides
It still works, but you have to know that dividing is the opposite of multiplying. Have a look at this example:
We want to remove the "4" | To remove it, do the opposite, in this case divide by 4: | Do it to both sides: | Which is ... | Solved! |
|
|
|
|
Solve this one:
x | / | 3 | = | 5 |
Start with: | x/3 = 5 |
What you are aiming for is an answer like "x = ...", and the divide by 3 is in the way of that! If you multiply by 3 you can cancel out the divide by 3 (because 3/3=1) |
|
So, let us have a go at multiplying by 3 on both sides: | x/3 ×3 = 5 ×3 |
A little arithmetic (3/3 = 1 and 5×3 = 15) becomes: | 1x = 15 |
Which is just: | x = 15 |
(Quick Check: 15/3 = 5) |
|
More Complicated Example
How would you solve this?
| x | / | 3 | + | 2 | = | 5 |
It might look hard, but not if you solve it in stages.
First let us get rid of the "+2":
Start with: | x/3 + 2 = 5 |
To remove the plus 2 use minus 2 (because 2-2=0) | x/3 + 2 -2 = 5 -2 |
A little arithmetic (2-2 = 0 and 5-2 = 3) becomes: | x/3 + 0 = 3 |
Which is just: | x/3 = 3 |
Now, get rid of the "/3":
Start with: | x/3 = 3 |
If you multiply by 3 you can cancel out the divide by 3: | x/3 ×3 = 3 ×3 |
A little arithmetic (3/3 = 1 and 5×3 = 15) becomes: | 1x = 9 |
Which is just: | x = 9 |
(Quick Check: 9/3 + 2 = 3+2 = 5) |
When you get more experienced:
When you get more experienced, you can solve it like this:
Start with: | x/3 + 2 = 5 |
Subtract 2 from both sides: | x/3 + 2 -2 = 5 -2 |
Simplify: | x/3 = 3 |
Multiply by 3 on both sides: | x/3 ×3 = 3 ×3 |
Simplify: | x = 9 |
Or even like this:
Start with: | x/3 + 2 = 5 |
Subtract 2: | x/3 = 3 |
Multiply by 3: | x = 9 |
Document Actions

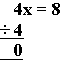
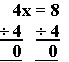
 Like us on Facebook
Like us on Facebook